I am Associate Professor for Machine Learning and Artificial Intelligence at TU Dortmund University and a faculty member of the Lamarr Institute for Machine Learning and Artificial Intelligence.
I remain affiliated with the Institute for Artificial Intelligence in Medicine (IKIM) at the University Medicine Essen, where I continue to collaborate on medical AI research. I offer Bachelor’s and Master’s thesis topics for students of the UA Ruhr (University of Duisburg-Essen, Ruhr-University Bochum, and TU Dortmund).
My Erdős number is at most 4.
News
- My PhD student Ting Han, my colleagues Linara Adilova, Henning Petzka, Jens Kleesiek, and I published a paper on “Flatness is Necessary, Neural Collapse is Not: Rethinking Generalization via Grokking” at NeurIPS 2025 (A*, top 7%)
- My colleagues Linara Adilova, Bruno Casella, Samuele Fonio, Mirko Polato and I are organizing the Workshop on Federated Learning in Critical Applications at AAAI, 2026 in Singapore.
- I have been appointed Associate Professor for Machine Learning and Artificial Intelligence at TU Dortmund University and joined the Lamarr Institute for Machine Learning and Artificial Intelligence. I will continue my research on deep learning theory, causality, and trustworthy federated learning, with a strong focus on medical and high-stakes applications.
- We are presenting two papers at AAAI 2025 (A*, top 7%): Amr Abourayya, Jens Kleesiek, Kanishka Rao, Erman Ayday, Bharat Rao, Geoffrey I. Webb, and I published a paper on “Little is Enough: Boosting Privacy by Sharing Only Hard Labels in Federated Semi-Supervised Learning” and Sebastian Dalleiger, Jilles Vreeken, and I published a paper on “Federated Binary Matrix Factorization using Proximal Optimization“.
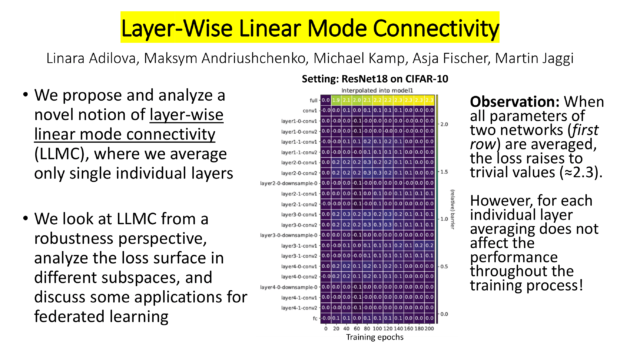
- My colleagues Linara Adilova, Maksym Andriushchenko, Asja Fischer, Martin Jaggi and I published a paper on Layer-wise Linear Mode Connectivity at ICLR 2024 (A*, top 7%).
- My colleagues Fan Yang, Pierre Le Bodic, Mario Boley and I published a paper on Orthogonal Gradient Boosting for Simpler Additive Rule Ensembles at AISTATS 2024 (A, top 16%).
Research Interests
My research focuses on the development of trustworthy and theoretically grounded machine learning methods—particularly in settings where data is distributed, privacy is critical, and model performance must be provable, interpretable, and robust. I am especially interested in the interplay between deep learning theory, causal representation learning, and federated learning, and how these foundations can be leveraged to design reliable AI systems for real-world, high-stakes applications such as healthcare.
I investigate the mathematical principles underlying deep learning, including loss surface geometry, generalization theory, and flatness, and study their connection to robustness and adversarial behavior. In parallel, I explore the discovery and utilization of causal structures in data—both to improve learning performance and to enhance model explainability and reliability. My group has pioneered methods for privacy-preserving causal discovery in federated settings, where both the statistical and ethical demands are uniquely high.
A core strand of my work centers around federated and decentralized learning, where models are trained collaboratively across devices or institutions without sharing raw data. I design algorithms that drastically reduce communication overhead, enable learning from highly non-IID or small datasets, and maintain data privacy while still achieving high performance. These approaches are rooted in online learning, optimization theory, and distributed systems, and are supported by rigorous guarantees.
In applied research, I collaborate closely with partners in medicine, industry, and government to ensure that theoretical advances translate into tangible impact. I have contributed to medical AI tools for early disease detection, 3D shape analysis, and transfer learning under domain shift—while rigorously addressing issues of privacy, fairness, and explainability. Beyond healthcare, my methods have been applied to autonomous driving, cybersecurity, and industrial automation.
At the Lamarr Institute, I contribute to Germany’s national mission of building ethical, trustworthy, and high-performance AI systems that are both scientifically excellent and socially responsible. My work is regularly published at the top conferences in machine learning, including NeurIPS, ICLR, and AAAI.
Curriculum Vitae – Highlights
Michael Kamp is Associate Professor for Machine Learning and Artificial Intelligence at TU Dortmund University and a faculty member of the Lamarr Institute for Machine Learning and Artificial Intelligence. His research spans the theoretical foundations of deep learning, causal representation learning, and trustworthy machine learning, with a particular focus on federated learning and privacy-preserving optimization. He develops machine learning methods that are not only mathematically rigorous but also designed to meet the demands of high-stakes real-world applications, particularly in healthcare and medicine.
He is also affiliated with the Institut für KI in der Medizin (IKIM) at the University Medicine Essen, where he previously led the research group Trustworthy Machine Learning. He continues to collaborate closely with IKIM on cutting-edge medical AI research at the intersection of clinical practice, data privacy, and reliable machine learning.
Earlier in his career, Michael was a postdoctoral researcher at the CISPA Helmholtz Center for Information Security in the Exploratory Data Analysis group of Jilles Vreeken (2021), and from 2019 to 2021 a postdoctoral fellow at Data Science & AI Department at Monash University and the Monash Data Futures Institute, where he remained an associated research fellow until 2024. Prior to that, he spent nearly a decade at Fraunhofer IAIS as data scientist, where he led the institute’s contributions to the EU project DiSIEM and headed a small applied research team working at the interface of academic research and industrial deployment. He also advised and trained corporate partners such as Volkswagen and DHL on data-driven innovation.
Michael Kamp received his doctorate from the University of Bonn, where he taught graduate seminars and supervised numerous theses. Prior to entering academia, he worked for over a decade as a professional software developer. He is a member of the editorial board of the Springer journal Machine Learning and a member of the ELLIS society.
Awards
- I received the NeurIPS 2021 outstanding reviewer award.
- I received a 2021 ICLR reviewer award.
- Our paper “Resource-Constrained On-Device Learning by Dynamic Averaging” won the Best Paper Award at the PDFL’20 workshop. Congratulations to Lukas, and our co-authors.
- I received the NeurIPS 2019 best reviewer award.
- I received the ICML 2019 reviewer award.