Disclaimer: this article is an advertisement for our workshop on parallel, distributed, and federated learning (PDFL’20) at ECMLPKDD this year and a call for contributions. First I wanted to just post the workshop description and be done with it, but then I thought I might add some actual content to give this article some actual value. Let’s see how that works out.
Distributed Machine Learning
Distributed machine learning is a huge topic since the Big Data hype. However, the landscape of machine learning applications is changing rapidly: large centralized datasets are replaced by high volume, high velocity data streams generated by a vast number of geographically distributed, loosely connected devices, such as mobile phones, smart sensors, autonomous vehicles or industrial machines. Current learning approaches centralize the data and process it in parallel in a cluster or cloud. This way, you again have a centralized dataset and can run your off-the-shelf efficient machine learning algorithm – think of Spark’s mllib, for example. And of course, a lot of really good research is done on how to improve machine learning in such a high-performance setup (e.g., the work of Janis Keuper). However, this has three major disadvantages: (i) it does not scale well with the number of data-generating devices since their growth exceeds that of computing centers, (ii) the communication costs for centralizing the data are prohibitive in many applications, and (iii) it requires sharing potentially privacy-sensitive data. Pushing computation towards the data-generating devices alleviates these problems and allows to employ their otherwise unused computing power.
Distributed Gradient Computation
The first more general parallelization scheme, i.e., one that is applicable to several ML algorithms at once, was the distributed mini-batch algorithm of Ofer Dekel and his colleagues from Microsoft (I think the idea precedes him, but he wrote the seminal paper). The idea is very simple: in any gradient based ML algorithm, e.g., stochastic gradient descent, you can calculate the gradients locally and send them to a coordinator node. The coordinator sums them up (which is theoretically sound, since the sum of local gradients is the gradient with respect to all local data points) and performs one update step with the summed up gradient. It then sends the updated model to the local nodes who compute the next round of gradients. There’s been extensive work on showing why this is theoretically sound, and it actually works in practice. The scalability of the approach is seemingly perfect, and it has even been called “embarrassingly parallel”, to underline how easy and effective the parallelization is. Since a lot of machine learning relies on gradient based methods, this technique is wide-spread, e.g., it is used in Spark’s mllib and in many implementations of the parameter server.
The Problem of Distributed Gradient Computation for ML
At this point, we could be done. Actually, during my PhD I at many points asked myself why I should work on other methods, since this is so effective. But the devil lies in the detail, and there are two large, connected issues with this technique. The first one is the amount of communication: for every update step, the locally computed gradients need to be send to the coordinator and the updated model has to be send back. This is no problem in a tightly connected system, like a high-performance cluster, but can already become an issue in a cloud, and is prohibitive for physically distributed devices, like cars and cellphones. So why not compute more local gradients each iteration and update a bit less frequently? On paper, this should solve the problem. Here comes the second, more severe issue into play. And for this one, I have to give a bit of background.
Two very prominent optimization algorithms used for machine learning are gradient descent (GD) and stochastic gradient descent (SGD). In gradient descent, you compute the gradient with respect to all samples in your dataset and then update your model, and keep iterating this until you converge. In stochastic gradient descent, you compute the gradient with respect to only a single sample and then update. In standard optimization settings, GD requires less updates, but each update is more costly, since you have to calculate all the gradients. SGD instead requires more updates, but each update is dirt cheap. There is also something in between, the mini-batch SGD: compute the gradient with respect to a hand full of samples (the mini-batch) and then update. The larger the mini-batch, the more this resembles GD, the smaller it is, the more it behaves like SGD.
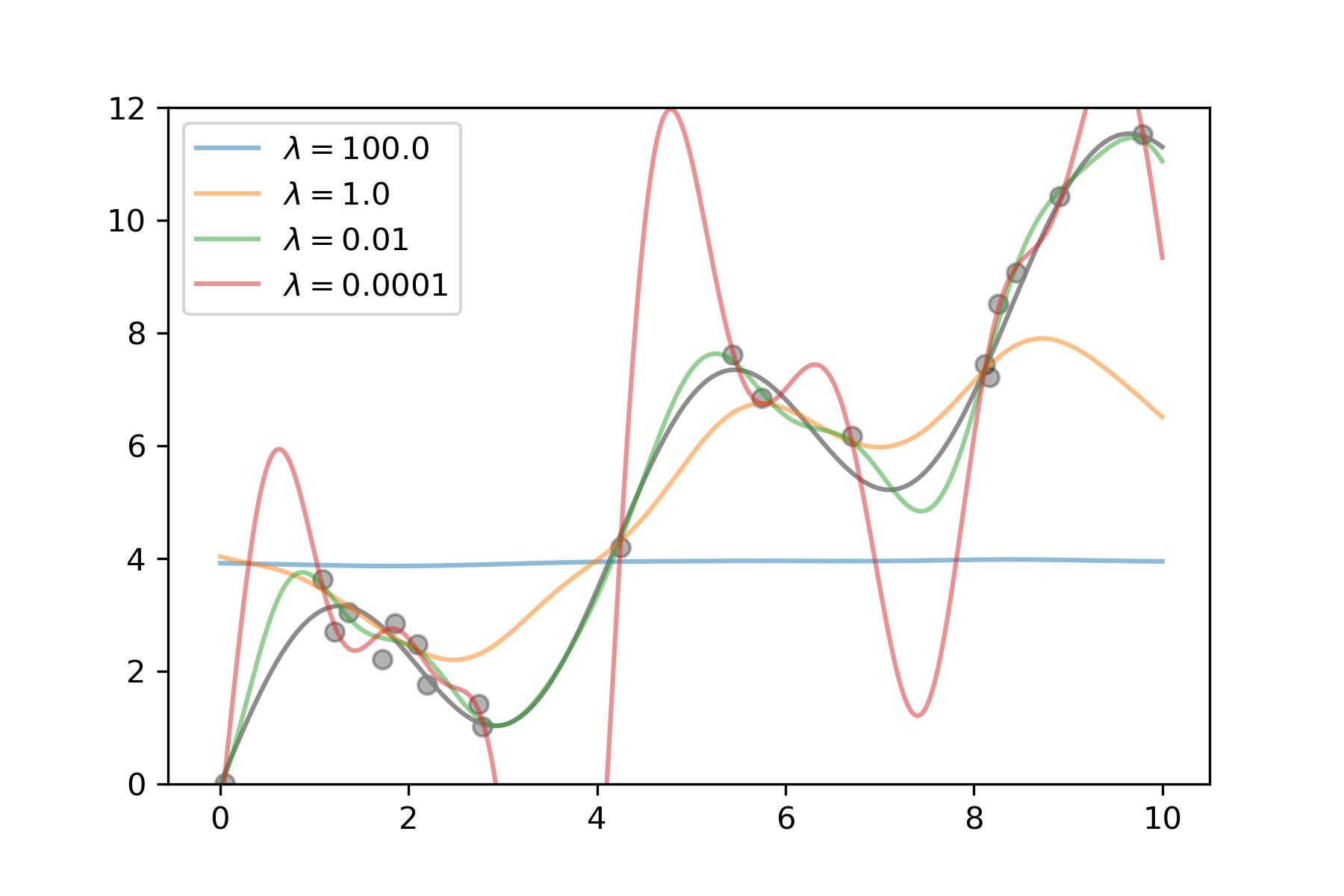
Figure 1: Support vector regression of a one-dimensional example (sinus with upward trend) trained on a sample of 20 points. The higher the regularization parameter lambda, the less complex the model gets, up to a horizontal line for lambda = 100. The smaller the parameter, the more complex the model becomes, eventually being able to fit nearly each sample point, but behaving wildly wrong in-between samples.
With machine learning, there is however an interesting twist to the story, and this one becomes more theoretical, so please bear with me. In machine learning, you want to optimize the risk, or true error of your model. That is, you want to minimize the error the model makes on novel, unseen data. This is also called the generalization error. All that you can do, however, is minimize the empirical error, that is, the error you make on your training set. However, simply finding the model that minimizes the empirical risk can lead to an effect called overfitting: if the model is complex enough, it can memorize the training set and achieve zero error there, but be completely wrong on everything else. What is typically done to avoid this is called regularization: you restrict the model complexity a bit to find a nice trade-off between empirical error and generalization. In figure 1 I illustrate this for support vector machines. Their complexity can be controlled with the regularization parameter lambda. If we regularize too much, the model is very simple and cannot fit the data, so both empirical and true error are high. If we regularize too little, the model becomes very complex and can fit each training point nearly perfectly, but in between it shows crazy behavior. The optimum is somewhere in the middle. Of course, finding this optimum is not trivial and has to be done empirically for each new dataset.
Ok, so why this lengthy digression into generalization? Because SGD has a very cool property: if you draw a new sample for every update, then in expectation, SGD optimizes the true error directly, not the empirical error (see Chapter 14.5.1 in this awesome book). So while GD is better at finding the model that minimizes the empirical error, SGD will find a model that does not minimize the empirical error, but generalizes a lot better. And indeed, this has been observed over and over, especially with neural networks. And now, finally, we get back to the problem with distributed mini-batching. When you calculate more gradients on each local device, the update is made with respect to more samples. So your “mini-batch size” becomes larger. But then, your learning algorithm behaves more like GD and not like SGD. So your model’s true error will become worse. And it’s not only the communication frequency, it’s also the number of nodes. If you have 10 nodes, and each one computes a single gradient, then the effective mini-batch size for your updates is 10. If you use 1000 nodes each computing a single gradient, the mini-batch size becomes 1000. So here is the gist: with distributed mini-batching you cannot scale up your system arbitrarily and you cannot reduce communication that much, because otherwise it will behave too much like GD and will produce models that do not generalize well. Short disclaimer at this point: I am sure that lots of people have worked on clever practical tweaks to alleviate this problem and I hope we will see some of these at our workshop. However, there is no principle way around it – at least I don’t know of one, so please correct me if I am wrong.
Model Averaging and Federated Learning
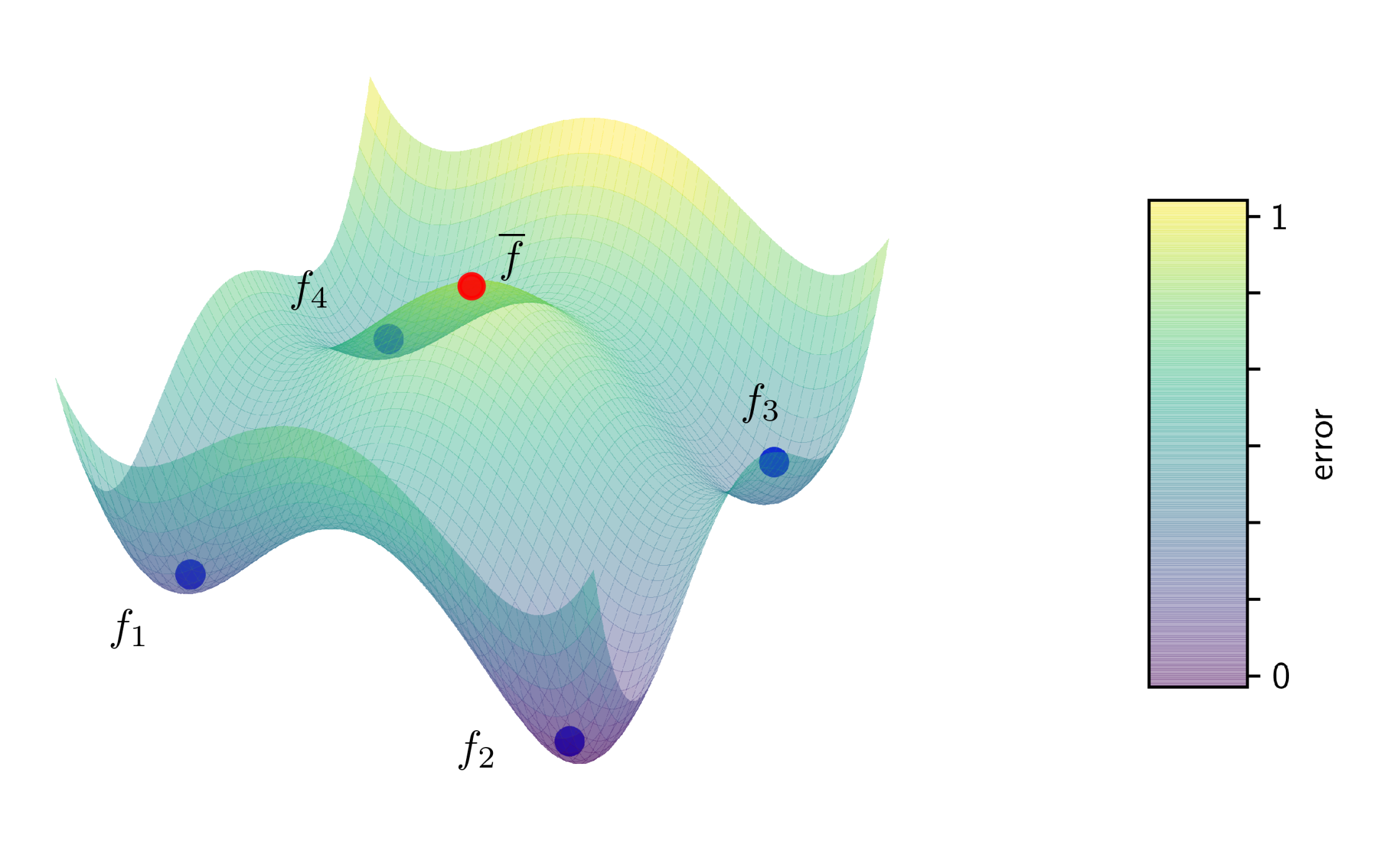
Figure 2: Illustration of a non-convex error surface with four models (blue) each having reached a local minimum. The average (red) of these models has a substantially higher error than any of the four local models.
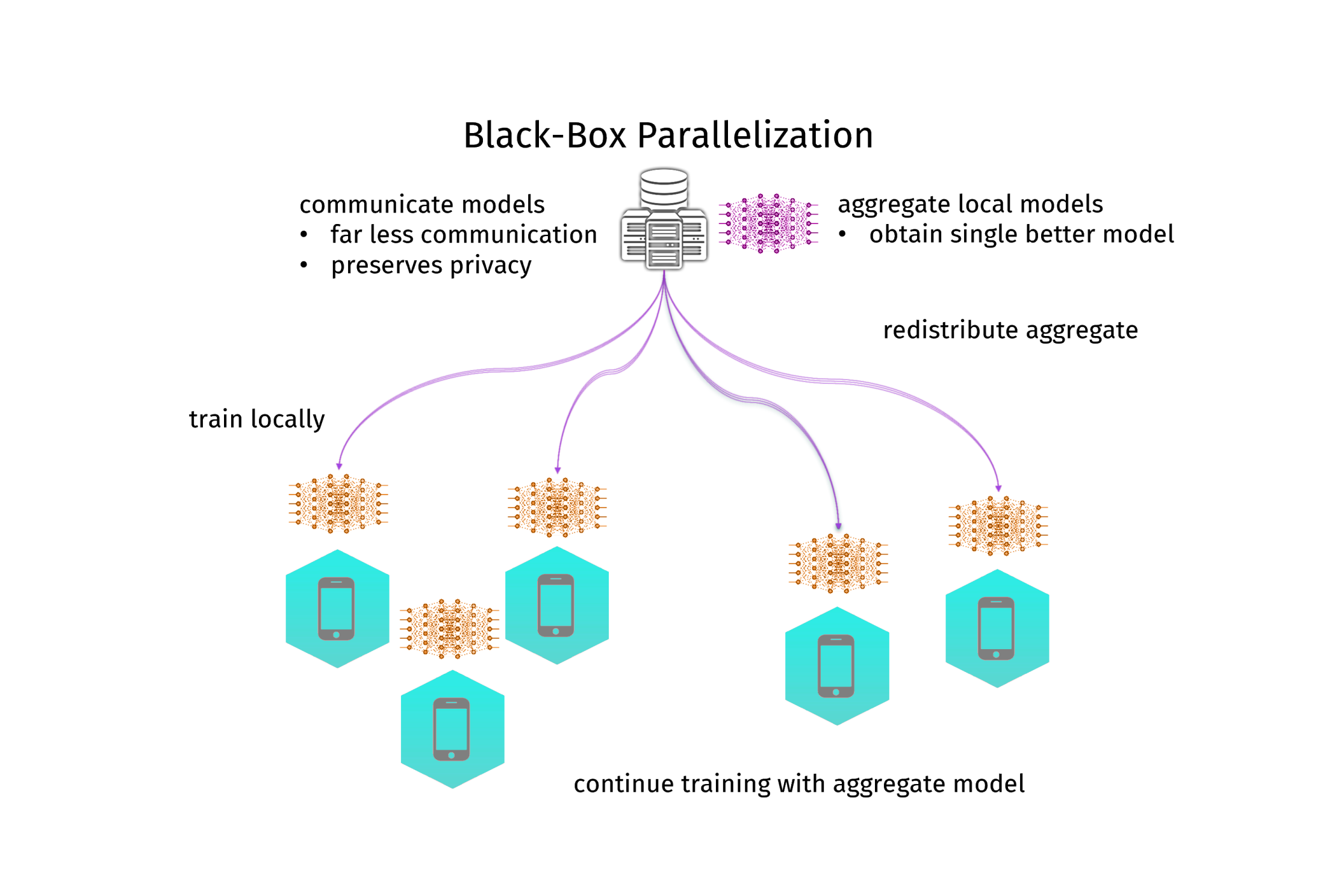
A different approach is to not parallelize the learning algorithm itself at all. Instead, you train a local model, send the model parameters to the coordinator and aggregate them into a better model (and then you could send that better model back and iterate the process). In my PhD-thesis I called this black-box parallelization, since it treats the learning algorithm as a black box. A simple but effective method to aggregate model parameters is to just average them. A lot of people where researching in this direction, but it was Google that brought the breakthrough in 2017 and gave this approach popularity, when they did averaging for neural networks and called it federated learning. This has created quite a hype around this topic, especially in the deep learning community. And indeed, it works. Google is using it to train their link recommendation models in their keyboard app for android phones. It uses less communication and is more resilient than distributed mini-batching. Moreover, this approach is highly privacy-preserving, and thus a hot candidate for machine learning in the medical domain. However, there is one big issue: the model you get by averaging is not necessarily the one you would get from centralized training. Instead, you always loose in model quality. And this time not only on the generalization ability, but actually also on the empirical error. It gets even worse: for neural networks there can be multiple minima of the empirical error, so the average of a bunch of models can be even a lot worse than the local models (see figure 2 for an illustration). In practice, this still works very well. Moreover, the communication can be further reduced by only communicating with a random subset of nodes (federated averaging), or by deciding in a data-driven manner when to communicate (dynamic averaging). And under some strict assumptions, one can even understand how it works theoretically.
Still, there is one subtle issue which might be a deal breaker. Let’s assume we learn using our off-the-shelf SGD which requires us to set a learning rate, let’s call that one l. It is the step size each update makes. To achieve good performance, this l has to be set correctly, not too small and not to large. If we choose it too small, the algorithm will take ages to converge to a good model. If we choose it too large, the algorithm will jump around wildly and might ultimately diverge, breaking the learning entirely. Now, what happens when you train two models separately, each with a learning rate l for exactly one update step and then average their parameters? You will get the same model you would get when training on both local datasets jointly, but with half the learning rate. If instead you used ten models, it would be one tenth the learning rate (see Prop. 3 in this paper on dynamic averaging for deep learning). So the learning rate goes down with the number of nodes in your distributed system. Now this is a huge problem! If you use too many nodes, your effective learning rate will be tiny and the model barely converges to a good one. One can compensate by setting higher learning rates at the local nodes – and this actually works – but it only goes so far; if you set the local learning rates too high, local training breaks completely and nothing works. This seems to put a limit on the scalability of the approach. I would love to see some analysis and ideas to overcome this in our workshop!
The Radon Machine
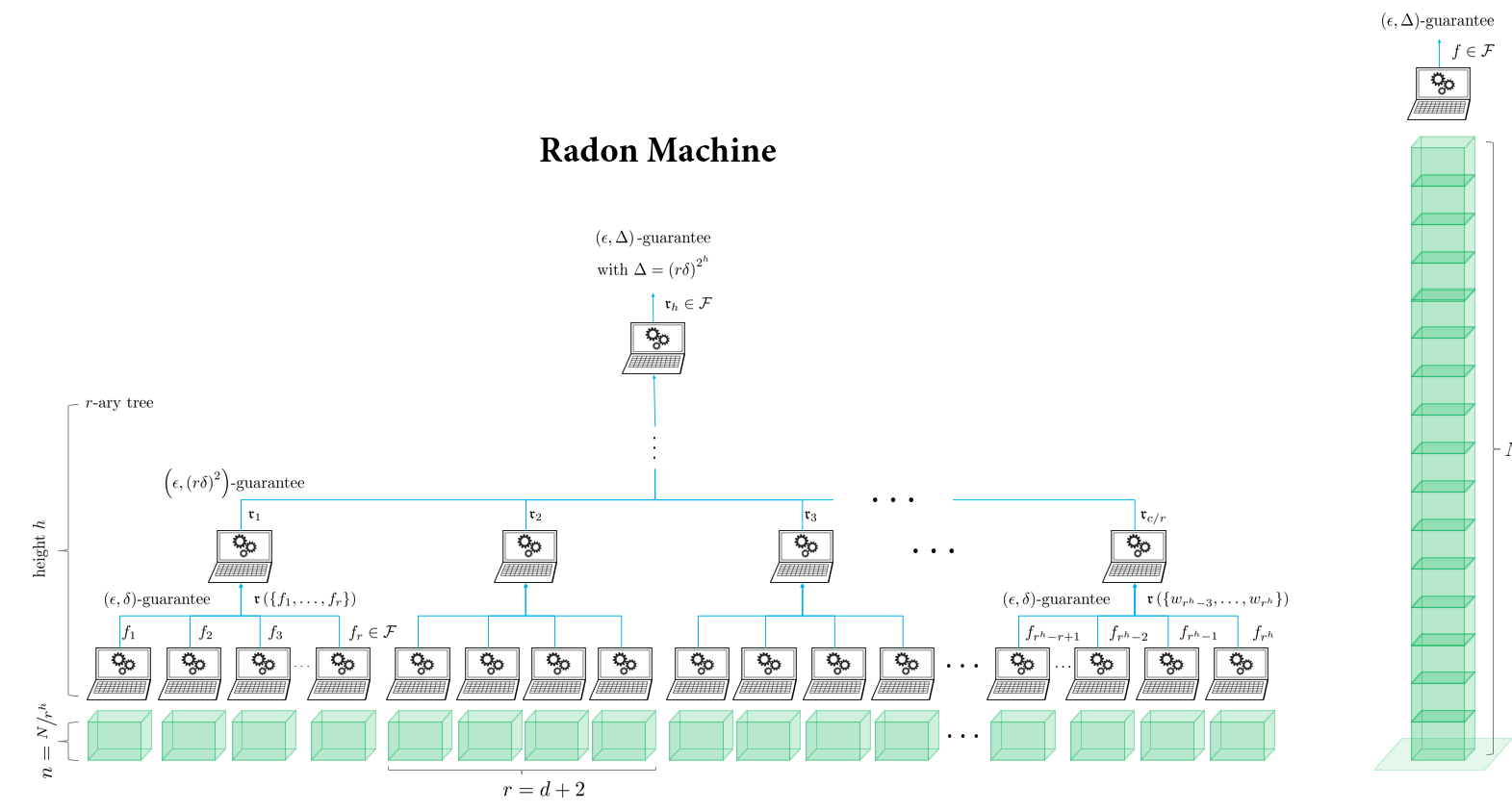
Finally, there is a more esoteric approach which does not average model parameters but iteratively calculates a form of high-dimensional median – called the Radon point – on them. The approach is called Radon machine and has some very nice theoretical properties. It scales well with the number of nodes, it gives a guarantee on the model quality, it is also privacy preserving, and it only requires a single round of communication. However, it currently only works for linear models and the guarantees only hold for convex learning problems. So its practical use is still quite limited. Still, going beyond averaging could be the way to overcome all these issues. I hope we can see some novel approaches along this line, as well.
Conclusion
So here we are: there are traditional distributed ML approaches that produce the same model as the centralized computation, but they require a prohibitive amount of communication and don’t scale well. Then there is distributed mini-batching, which computes gradients in parallel. This is working well in tightly coupled systems like high-performance clusters, but works not so well on physically distributed devices and doesn’t arbitrarily scale. Then there is model averaging, which works well in practice, but is not well understood theoretically, and seems to have an in-built limit to its scalability. And then there is the Radon machine, which is theoretically interesting, but limited to convex methods and linear models, so at its current stage it is not very useful in practice. Thus, despite the surge of papers in this phase of hype, there is still a lot to do. And with this, I will now blatantly advertise our workshop.
Workshop on Parallel, Distributed, and Federated Learning – PDFL’20
Call for Papers:
Workshop website: https://pdfl.iais.fraunhofer.de/
Important Dates:
- Submission deadline: 9 June 2020
- Acceptance notification: 9 July 2020
- Camera-ready deadline: 26 July 2020
- Workshop: TBA