Tag Archives: linear mode connectivity
Layer-Wise Linear Mode Connectivity
Linear mode connectivity describes a phenomenon observed for neural networks where every linear interpolation between two trained neural networks has roughly the same loss. In other words, there is a rather flat line in the loss surface connecting the two networks.
We know that linear mode connectivity (LMC) doesn’t hold for two independently trained models. But what about layer-wise LMC? Well, it is very different! Our new work “Layer-wise linear mode connectivity” published at ICLR 2024 explores this and its applications to federated averaging. This is joint work led by Linara Adylova, together with Maksym Andriushchenko, Asja Fischer, and Martin Jaggi.
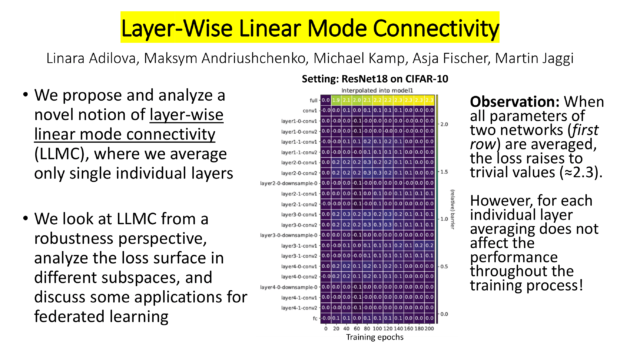
We investigate layer-wise averaging and discover that for multiple networks, tasks, and setups averaging only one layer does not affect the performance (See Fig. 2). This is in line with the research of Chatterji, at al. [1] showing that reinitialization of individual layers does not change accuracy.
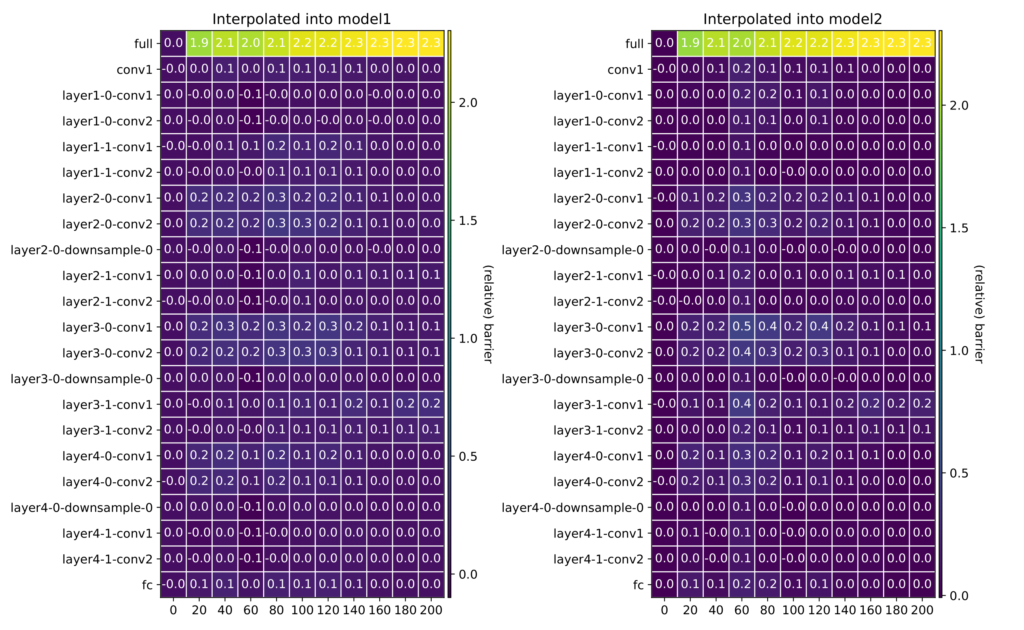
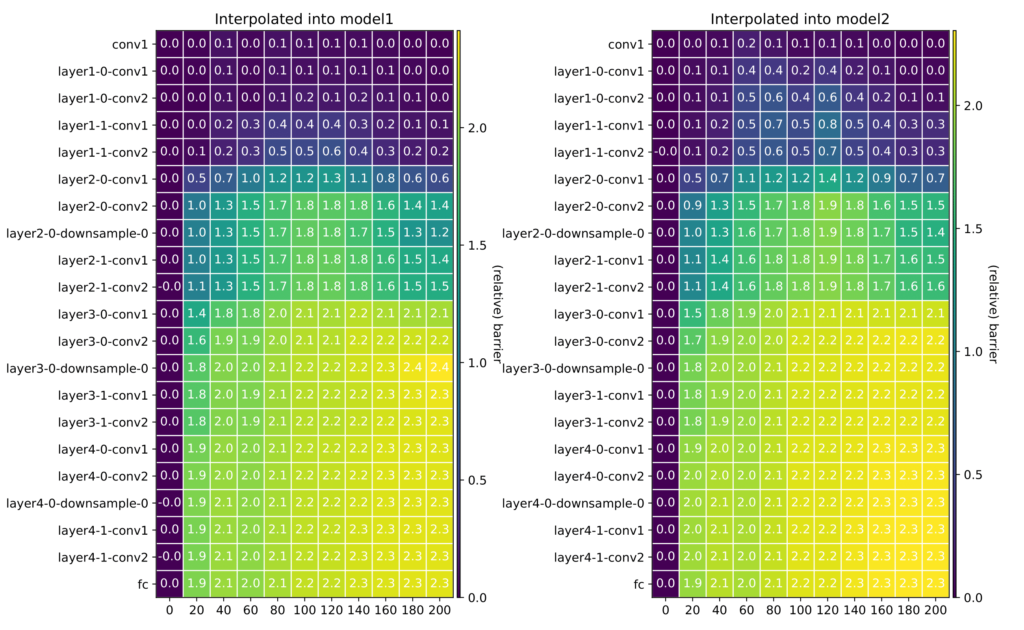
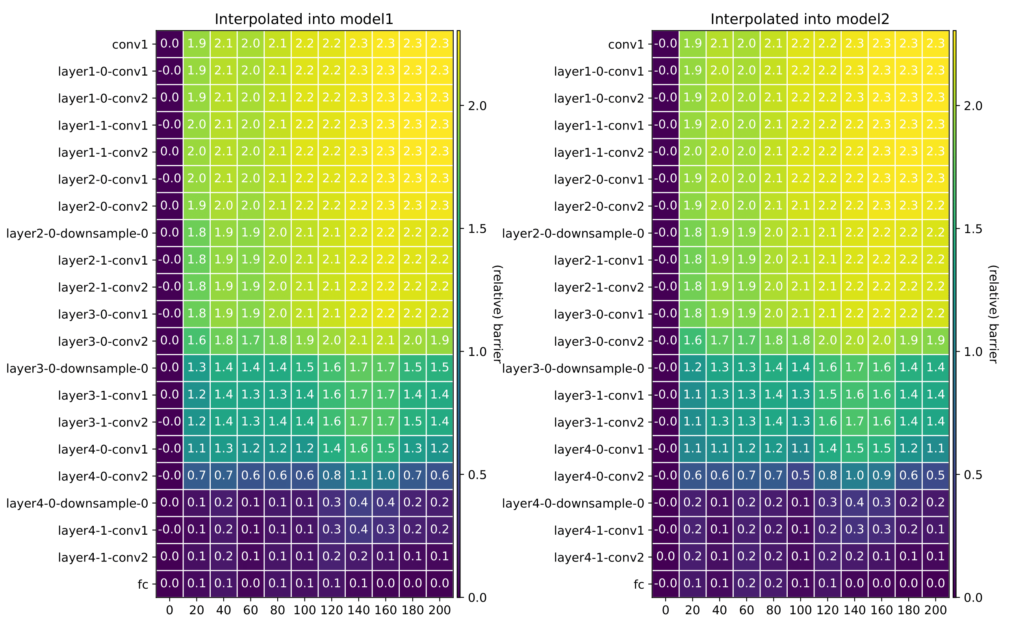
Nevertheless, one might as whether there is some critical amount of layers needed to be averaged to get to a high loss point. We investigated this in Fig. 3 by computing the barrier when interpolating between the first layers of the two networks, then the first and second layer, and so on (left). We did the same starting from the bottom, interpolating between the last layers, then the last and penultimate layers, and so on (right). It turns out that barrier-prone layers are concentrated in the middle of a model.
Is there a way to gain more insights on this phenomenon? Let’s see how it looks like for a minimalistic example of a deep linear network (Fig. 4). Ultimately, a linear network is convex with respect to any of its layer cuts. This example demonstrates how the interpolation between the full networks leads to a barrier, while interpolating only the second layer leads to a much lower loss barrier. Interpolating only the first layer, however, leads to a high loss barrier, consistent with our experiments on deep non-linear networks.
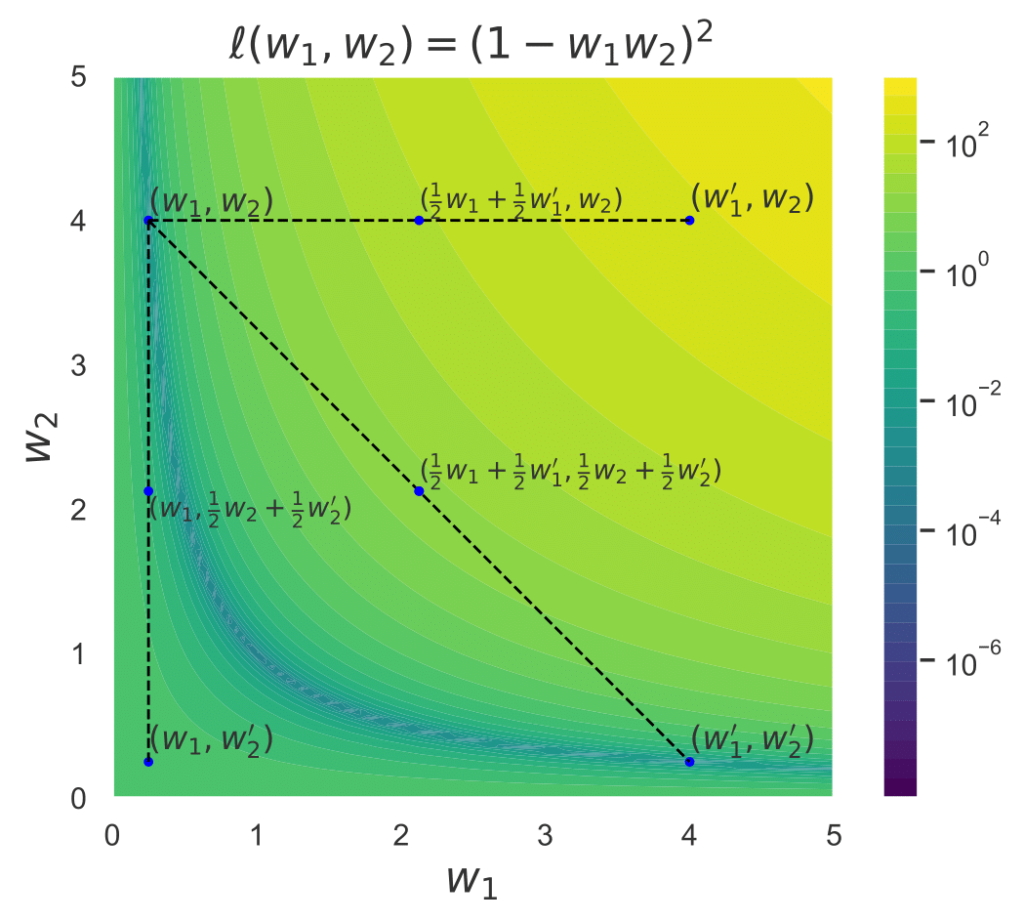

Can robustness explain this property? That is, do all the neural networks have a particular weight changes robustness that allows to compensate for one layer modifications? Or is the interpolation direction somehow special? We tested the robustness to random perturbations of each layer in Fig. 5. Our results show that for some layers there is indeed a robustness against perturbations. Moreover, the more robust the model is in general, e.g., because being in a flat minimum [2], the harder it is to get a high loss through perturbations. However, we do not see the same behavior of layers for random perturbation that we see for the interpolation between two networks. This indicates that the interpolation direction is indeed somehow special.
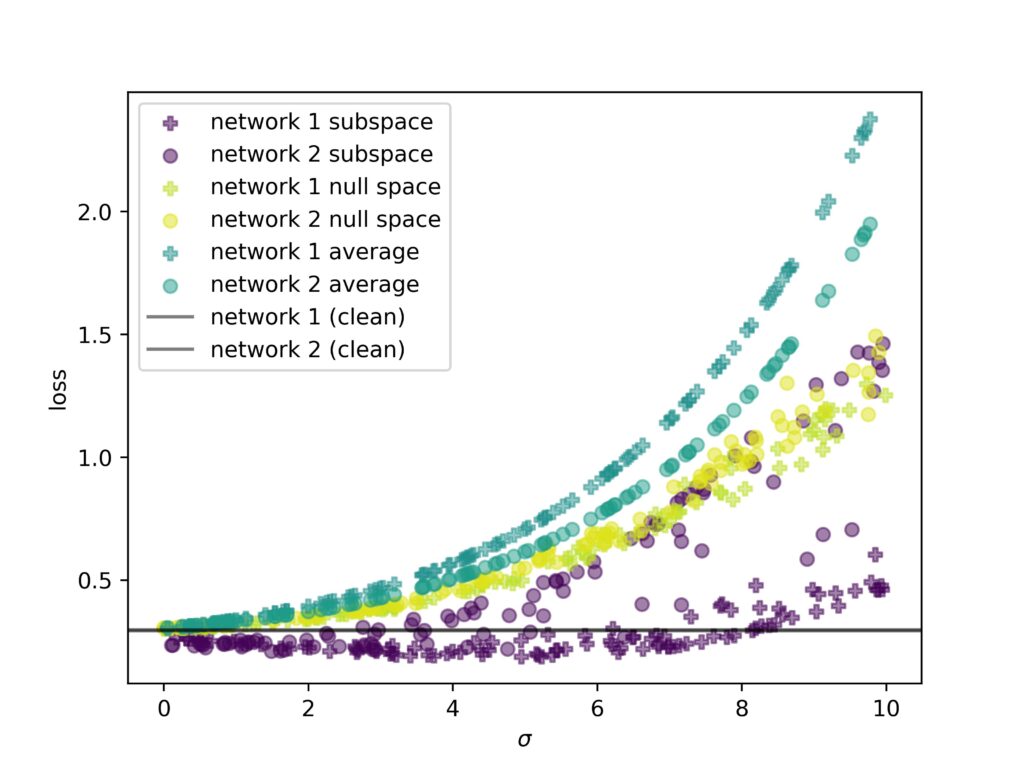
This means, we cannot treat random directions as uniformly representative of the loss surface. To investigate this further, we analyze how loss in different directions impacts the loss of a network. We distinguish three separate directions: (i) a random perturbation along the interpolation direction, (ii) in the training subspace, i.e., the space spanned by the two networks during training, and (iii) the null space, i.e., the subspace perpendicular to the training subspace. Our experiment in Fig, 6 shows that particular subspaces are more stable than others. Especially, the interpolation direction is susceptible to noise.
In summary, we investigate the fine-grained structure of barriers on the loss surface observed when averaging models. We propose a novel notion of layer-wise linear mode connectivity and show empirically that on the level of individual layers the averaging barrier is always insignificant compared to the full model barrier. We also discover a structure in the cumulative averaging barriers, where middle layers are prone to create a barrier, which might have further connections to the existing investigations of the training process of neural networks.
It is important to emphasize that the definition of barrier should be selected very carefully: When performance of the end points is very different, comparing to the mean performance might be misleading for understanding the existence of barrier. Our explanation of LLMC from the robustness perspective aligns with previously discovered layer criticality [3] and shows that indeed more robust models are slower to reach barriers. Training space analysis indicates that considering random directions on the loss surface might be misleading for its understanding.
Our research poses an interesting question: How is the structure of barriers affected by the optimization parameters and the training dataset? We see a very pronounced effect of learning rate and in preliminary investigation we observe that easier tasks result in less layers sensitive to modifications. Understanding this connection can explain the effects of the optimization parameters on the optimization landscape.
References:
[1] Niladri S Chatterji, Behnam Neyshabur, and Hanie Sedghi. The intriguing role of module criticality in the generalization of deep networks. In International Conference on Learning Representations, 2020.
[2] Henning Petzka, Michael Kamp, Linara Adilova, Cristian Sminchisescu, and Mario Boley. Relative flatness and generalization. In Advances in Neural Information Processing Systems, 2021.
[3] Zhang, Chiyuan, Samy Bengio, and Yoram Singer. “Are all layers created equal?.” The Journal of Machine Learning Research 23.1 (2022): 2930-2957.
For more information, check out my research group on Trustworthy Machine Learning at the Institute for AI in Medicine (IKIM) and the Institute for Neuroinformatics at the Ruhr University Bochum.